Jeszcze będąc na studiach próbowałem zbudować sobie wyobrażenie analiz i procesu decyzyjnego w branży logistycznej. Wydawało mi się to czymś skomplikowanym czego nie potrafiłem pojąć, bo myślałem, że w środowisku profesjonalistów wykorzystuje się bardzo zaawansowaną wiedzę
i narzędzia, a wnioskowanie wymaga ogromnego doświadczenia i wyczucia. Jakże duże było moje zaskoczenie, gdy rozpocząłem swoją karierę. Nagle okazało się, że nie ma zaawansowanych algorytmów i narzędzi. Za to jest Excel i liczenie średniej arytmetycznej.
Spłynęła na mnie wówczas duża ulga, ponieważ moje obawy o byciu najsłabszym ogniwem stały się niezasadne. Po prostu wystarczy liczyć średnią!
No i w ten sposób przez pierwsze miesiące zadowolony liczyłem średnią i wyciągałem wnioski wprost proporcjonalne jakościowo do mojego doświadczenia, wyczucia i zastosowanej metody.
Szybko jednak powróciło do mnie przeczucie, że coś jest nie tak, że średnia to za mało. Wówczas postanowiłem rozbudować moje zdolności analityczne o nowe narzędzia i zastosowanie prawdziwej statystyki. Okazało się, że trafne wnioskowanie i budowanie wyobrażenia o rzeczywistości procesowej na podstawie danych jest znacznie bardziej skomplikowane niż sprowadzanie wszystkiego do średniej. Dostrzegłem również dwie prawidłowości:
-
- Im bardziej znamy się ze statystyką, tym lepsze wnioski wyciąga się z danych, nawet takich, które na pozór mówią dość mało.
-
-
- Im bardziej znamy się ze statystyką, tym mniej osób rozumie i/lub ufa wyciągniętym przeze mnie wnioskom, ponieważ nie rozumieją jak do nich doszedłem.
Tak więc zagoniłem się w przeciwny róg, czyli taki, gdzie ja umiem wyciągnąć wnioski za pomocą metod statystycznych, ale nikt nie rozumie skąd one się wzięły, a to z kolei skutkuje brakiem zaufania odbiorców do tych wniosków. To właśnie dlatego spotykamy się na tym blogu, którego misją jest zwiększenie świadomości nt. wnioskowania i analityki w środowisku logistycznym.
Wobec tego ten wpis będzie o rzeczach najbardziej podstawowych, czyli o miarach, które pozwalają nam opisać lub zrozumieć posiadany zestaw danych. Ten zakres w statystyce nazywa się statystyką opisową.
Statystyka opisowa jest to dziedzina statystyki pozwalająca opisać, podsumować i przeanalizować dane w sposób dający ogólne zrozumienie, co one reprezentują i jak one wyglądają. Innymi słowy umożliwiają nam zrozumieć jakie są cechy charakterystyczne naszych danych bez konieczności wykonywania skomplikowanych analiz. Ta część statystyki przede wszystkim pomaga w codziennych sytuacjach, gdy chcemy wyciągnąć szybkie wnioski z dużego zbioru danych.
Miary w statystyce opisowej dzielą się m.in. na miary tendencji centralnej i miary zróżnicowania. Te zaś dzielą się na miary klasyczne i pozycyjne.
Miary tendencji centralnej
Miary tendencji centralnej to to, czego najczęściej używamy intuicyjnie. Te miary mają pomóc nam opisać cały zbiór danych jedną wartością, która w założeniu ma stać gdzieś pośrodku. Aby oddać należne miejsce używanej przez wszystkich i wynoszonej na piedestał średniej, zacznijmy właśnie od niej. Średnia jest tzw. miarą klasyczną, co oznacza, że jej wartość wynika bezpośrednio z liczb, które mamy w zestawie danych. W przeciwieństwie do innych miar, które mogą odnosić się do pozycji liczb w uporządkowanym zbiorze (np. mediana), średnia opiera się na wszystkich liczbach w zestawie
i ich wartości.
Wśród miar pozycyjnych miarą tendencji centralnej jest mediana.
Pewnie teraz zaczyna pojawiać się w głowach pytanie
„No dobra średnią znam, medianę jako tako, ale skąd mam wiedzieć, kiedy używać której miary?”
Śpiesząc z odpowiedzią, zacznijmy od prostego przykładu. Załóżmy, że mamy magazyn, w którym przez 12 miesięcy w roku wydajemy towar. Podane na wykresie wartości to liczba wydanych palet. Jak widać przez niemal cały rok wartości nie odbiegają mocno od siebie i nie przekraczają 170, ale w grudniu biznes mocno się rozkręca i liczba wydań wzrasta do 5000 palet.

Rys. 1. Wielkość wydań towaru dla omawianego przykładu. Źródło: Opracowanie własne
Wyliczając średnią uzyskamy wynik około 519 palet. I w tym przypadku marnie nam to pokazuje tendencję centralną, ponieważ średnia odbiega dosyć mocno od tego jak realnie układają się wydania. Powodem jest wartość 5000 w grudniu, która jest wartością odstającą, czyli taką, która wyraźnie odbiega od pozostałych wartości (tzn. jest znacznie większa lub mniejsza od pozostałych). Miary klasyczne takie jak średnia są bardzo wrażliwe na wszelkie wartości odstające. Dlatego zanim policzymy średnią musimy się upewnić czy to na pewno prawidłowa miara. Reasumując, średnia może dawać niemiarodajne wyniki w przypadku, gdy jest liczona na podstawie danych zawierających wartości odstające.
Teraz pewnie się pojawi pytanie, skoro nie średnia, to co? No w takim przypadku lepiej użyć mediany. Mediana to wartość, która leży pośrodku posortowanych rosnąco wartości. Nie bazuje więc bezpośrednio na wielkościach wydań, a na pozycji w posortowanym zbiorze danych.
Więc przejdźmy krok po kroku, żeby lepiej zrozumieć co z tą medianą:
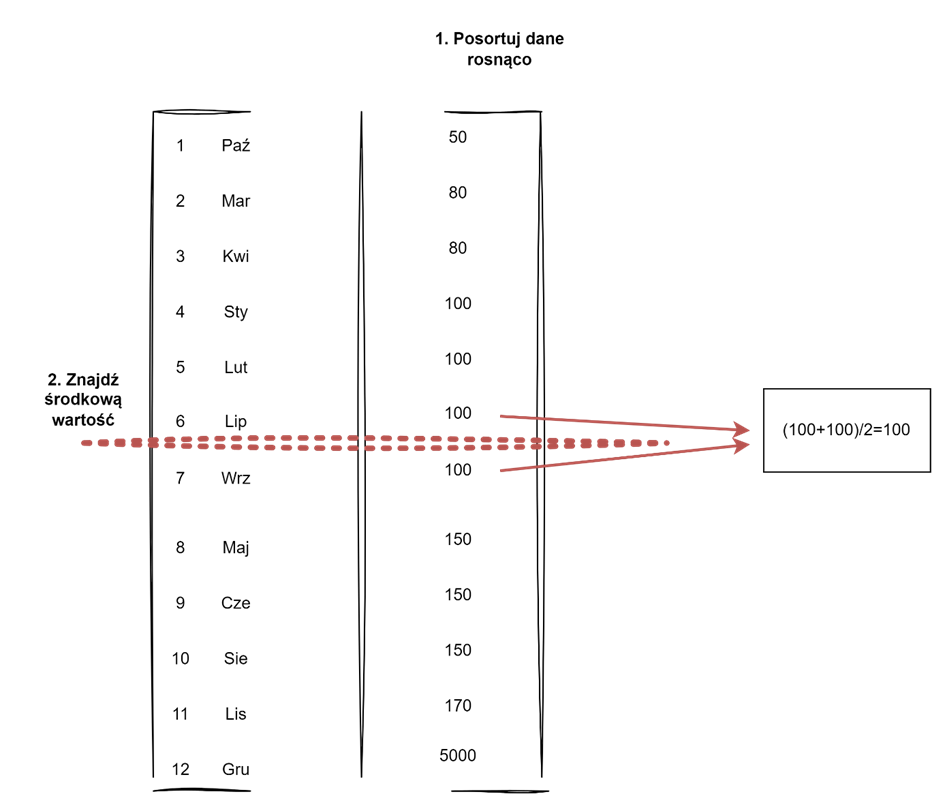
Rys. 2 Wizualizacja kroków niezbędnych do obliczenia mediany. Źródło: opracowanie własne
Aby znaleźć wartość środkową sortujemy nasz zbiór danych rosnąco. I z tak posortowanego zbioru wybieramy tę wartość, która stanowi jego środek. W naszym przypadku środek wypada pomiędzy wielkościami wydań z lipca i września. Na środku postawiłem linię, która przecina zbiór danych na dwa kawałki. Na górze mamy 6 wartości i na dole 6 wartości. Naszą medianą będzie wartość wyznaczona jako środek pomiędzy wartościami z lipca
i września. Upraszczając, liczymy po prostu średnią z tych dwóch wartości. Czyli nasza mediana wynosi 100 palet.
UWAGA. To jest przykład, który zawiera parzystą liczbę obserwacji (tzn. jest parzysta liczba miesięcy). W takim przypadku podział zbioru danych na dwie części będzie zawsze wypadał gdzieś pomiędzy dwoma wartościami. Dlatego liczymy średnią z dwóch wartości. Jeśli nasz zbiór danych ma nieparzystą liczbę obserwacji – dobrym przykładem jest tydzień (7 dni) – wówczas środek zbioru wypada bezpośrednio na jakimś konkretnym dniu tygodnia, tak więc nie ma potrzeby liczenia średniej, wystarczy potraktować tę wartość jako medianę,
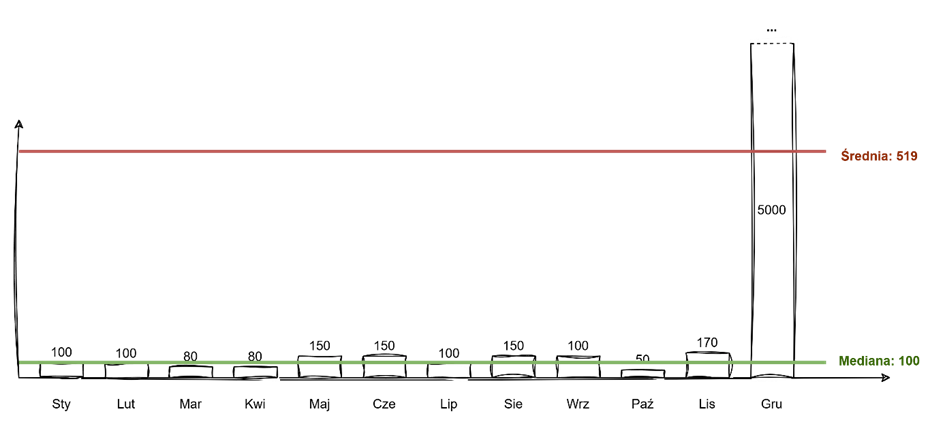
Rys. 3. Wyniki średniej i mediany naniesione na wizualizację wielkości wydań. Źródło: Opracowanie własne
I spójrzcie teraz. Bardzo dobrze widać, że mediana lepiej opisuje tendencję centralną tego zbioru danych. Przy takim rozkładzie mówiąc, że nasz magazyn wydaje przeciętnie 100 palet opisujemy rzeczywistość trafniej niż gdy powiedziemy, że ów magazyn wydaje średnio ponad 500 palet.
Na tym etapie warto również wspomnieć, że istnieją również kwartyle. Kwartyle wykorzystują ten sam mechanizm co mediana tylko dzielą nasz zbiór danych w innych miejscach.
Wyobraźmy sobie, że dzielimy nasze posortowane rosnąco dane na 4 równe części. Kwartyle to wartości, które występują na granicach tych części.
I zupełnie tak samo jak w przypadku mediany znaczenie ma tutaj to czy nasz zbiór danych ma parzystą czy nieparzystą liczbę wierszy.

Rys. 4. Podział zbioru danych na kwartyle. Źródło: Opracowanie własne
Zależności między średnią i medianą a dane
Spójrzcie teraz na porównanie z innym przykładem. Zestawmy nasze obecne dane z danymi z innego magazynu, którego wydania kształtują się w następujący sposób:
Styczeń: 400 palet
Luty: 600 palet
Marzec: 650 palet
Kwiecień: 450 palet
Maj: 400 palet
Czerwiec: 530 palet
Lipiec: 540 palet
Sierpień: 480 palet
Wrzesień: 500 palet
Październik: 550 palet
Listopad: 600 palet
Grudzień: 529 palet
Średnia w obu przypadkach kształtuje się na tym samym poziomie, czyli 519. W drugim magazynie wielkości wydań są trochę bardziej zrównoważone przez co średnia i mediana będą miały zbliżone do siebie wartości. To jest jedna, ze wskazówek, która pozwoli Wam zweryfikować czy użycie średniej jest ok. Mam tu na myśli, że im większa różnica między średnią a medianą tym jaśniej powinna nam się zapalić w głowie lamka na temat rozkładu danych i potencjalnie fałszywych wyników uzyskiwanych przez liczenie średniej.

Rys. 5. Porównanie wartości miar tendencji centralnej dla dwóch magazynów z tą samą średnią. Źródło: Opracowanie własne
Ogólnie prawidłowość jest taka, że jeśli średnia i mediana są bardzo blisko siebie, można przyjąć, że zestaw liczb jest dość stabilny i średnia dobrze opisuje całość. W takim przypadku, użycie średniej w obliczeniach będzie pomocne. Jednak często średnia i mediana mogą się wyraźnie różnić –
np. gdy kilka bardzo dużych lub bardzo małych wartości „przesuwa” średnią w jedną stronę. Wtedy lepiej posługiwać się medianą, ponieważ ona trafniej pokaże, co jest „typowe” dla naszego zestawu liczb i nie będzie aż tak zaburzona przez te skrajne wartości.
Pamiętajcie, że te miary przede wszystkim pomagają nam zrozumieć posiadane dane. Niekoniecznie nadają się do prognozowania. Prognozowanie to zupełnie inna dziedzina , która jest na tyle szeroka, że może powstać o niej niejeden wpis.
Zakończenie
Na tych miarach zakończymy ten wpis. Z pewnością odpoczynek się przyda by dobrze przyswoić to, co zostało podane w tym wpisie.
W kolejnym wpisie skupimy się na miarach zróżnicowania oraz interpretacji wyników miar tendencji centralnej w parze z miarami zróżnicowania.
Do zobaczenia!
Źródła
- Marek Ręklewski: Statysytka Opisowa. Teoria i przykłady, Włocławek, 2020.
- Peter Bruce, Andrew Bruce, Peter Gedeck: Statystyka praktyczna w data science. 50 kluczowych zagadnień w językach R i Python. Wydanie II, Helion, 2021